Típicament, per a jugar a escacs, els ordinadors han fet servir el teorema de Minimax de John von Neumann. Aquest teorema s'aplica per a jocs d'imformació perfecta entre dos adversaris, amb suma zero, establint que n'hi ha una estratègia que permet a tots dos jugadors minimitzar la pèrdua màxima esperada.
El jugador juga, doncs, amb l'estratègia que resulta en la minimització de la seva màxima pèrdua, considerant totes les respostes possibles del jugador adversari i la pèrdua màxima que pot comportar.
Si fos possible estudiar tot l'arbre de jugades, és a dir, totes les possibles jugades futures, es podria determinar una estratègia guanyadora; en la pràctica això és impossible. Va ser Claude Shannon en el seu text sobre escacs de 1950 Programming a Computer for Playing Chess
qui proposà limitar la profunditat de la recerca en l'arbre de possibilitats, determinant llavors el seu valor mitjançant una funció heurística.
La funció d'avaluació: heurístic
L'algorisme requereix, doncs, l'ús d'un heurístic, una funció d'avaluació d'una posició, una vegada s'ha fet l'exploració de les diferents jugades possibles, de manera que es pugui determinar quina és la millor. L'heurístic més evident consisteix en considerar el valor de les fitxes de cada jugador, però incorporar conceptes de posició en l'heurístic no és senzill, i requereix traspassar els coneixements d'un expert.
La profunditat de cerca és un límit de visibilitat que s'intenta
sobrepassar amb un heurístic, però els errors en aquesta estimació es propaguen cap amunt. En l'imatge d'Evolving Neural Networks to Focus Minimax Search es visualitza l'efecte horitzó provocat per la profunditat de búsqueda, i com l'error provocat per l'aplicació de l'heurístic es propaga. En l'imatge els quadrats fan càlcul del valor màxim, i cercles el mínim.
El gran problema de l'algorisme minimax és la seva dependència de l'heurístic, doncs el valor d'aquest heurístic té un factor d'error que es propaga cap amunt, i pot comportar errors en el resultat final de l'algorisme.
Aquest heurístic és doncs una funció fonamental en l'avaluació minimax, i és difícil establir una funció que no deixi descuidat algún punt; la correcció d'aquests defectes de l'heurístic s'aconsegueix fent un anàlisi amb una profunditat més gran, intentant obtenir una valoració més certera.
A més, aquesta funció d'avaluació (heurístic) és difícil de determinar en situacions poc estables, en situacions d'escac o situacions on existeix una amenaça a una peça. Aquest concepte d'estabilitat es denomina quiescència, i l'algorisme explora en major profunditat fins trobar un estat que compleix la quiescència, per poder avaluar correctament l'heurístic.
Extensió de la búsqueda
Per a certes jugades interessants es pot extendre la búsqueda en més profunditat; és un concepte una mica diferent de la quiescència, però de vegades la pot remplaçar, doncs la funció de l'extensió per a la quiescència és trobar una posició avaluable, sense amenaces que puguin desvirturar el resultat de l'heurístic, però l'extensió de la búsqueda pretèn analitzar en profunditat una posició que sembla interessant. Aquesta tècnica es va fer servir ampliament en Deep Blue, però actualment n'hi ha més interés en retallar les jugades poc interessants que en extèndre l'anàlisi de les interessants.
L'extensió de búsqueda es pot fer servir per analitzar situacions de: escac, situació amb pocs moviments possibles, seguretat del rei crítica, peons que coronen o es troben aprop de fer-ho, anàlisi per a amenaces detectades (generalment amb la tècnica del moviment null, que es detalla més endavant)...
Cost de l'algorisme
El cost de l'algorisme és O(bd), sent b el factor de ramificació, quantes jugades diferents possibles es poden fer en promig, i d la profunditat d'exploració, és a dir, quants nivells en davant s'exploren. Es escacs el valor per a b és lleugerament superior a 30, de vegades estimat fins i tot com a 36; explorant quatre nivells ja es requereixen més d'un milió i mig d'avaluacions, en cinc nivells més de 60 milions, i en sis nivells més de 2_100 milions.
El factor de ramificació b per a C'escacs és quatre vegades superior als escacs, aproximadament 144, fent que quatre nivells d'exploració comportin més de 400 milions d'avaluacions, en comptes d'un milió i mig. L'increment en el nombre d'avaluacions és degut a diversos factors: un escaquer més gran, més fitxes per a cada jugador i moviments addicionals deguts a la geometria hexagonal. En termes de profunditat d'exploració, comporta el cost d'un nivell i mig addicional comparat amb els escacs ortodoxos; és a dir, que per a explorar 5 nivells es requereix avaluar gairebé 62_000 milions de nodes.
Les taules de transposició
La gran quantitat de moviments que s'han d'analitzar comporta que es donin repeticions degudes a l'execució de moviments en diferent ordre; aquest fenòmen és en realitat força freqüent només cal que recordem que s'han d'analitzar tots els moviments possibles, i per a cada moviment possible, tots els moviments possibles, i així successivament degut a la transposició de l'ordre en què es realitzen els moviments. La repetició de posicions és fins i tot un problema, particularment en l'anàlisi de finals, quan queden poques fitxes en joc, doncs l'ànalisi de moviments podria acabar analitzant un cicle de les mateixes posicions si no es detecta la repetició que tanca el cicle.
Aquesta tècnica també es fa servir per aplicar la regla de repetició de posició, que permet a un jugador exigir taules si la mateixa posició es repeteix tres vegades, i en qualsevol cas seran taules quan una mateixa posició es repeteix cinc vegades.
Les posicions ja valorades s'emmagatzemen, i a més de la valoració per no haver de repetir els càlculs, es pot afegir informació com la millor jugada seleccionada, la profunditat on s'ha estudiat la posició... formant les taules de transposició. Aquestes taules s'emmagatzemen com a taules hash, que fan servir una clau, generalment un número de 64 bits en realitat 64 bits encara és un número massa gran per a indexar la taula, i com a índex es fa servir una reducció d'aquest valor, mòdul una potència de dos, que es calcula com a un valor únic o signatura associada a la posició, típicament fent servir tècniques com les fórmules de Zobrist, què faciliten la seva manipulació amb operacions xor.
Profundidad iterativa i control del temps
El gran problema és que la búsqueda minimax és una búsqueda en profunditat, és a dir, que s'explora una branca fins la profunditat establerta, abans de començar a explorar una altra branca. Aquesta estratègia resulta funesta quan el programa ha de tenir control del temps, doncs és molt difícil estimar el temps que pot costar l'anàlisi només fixant la profunditat, i si s'interromp l'anàlisi poden quedar encara alternatives importants per explorar.
La profundidad iterativa crida repetidament a una rutina de cerca augmentant la profunditat, fins a aconseguir el valor desitjat. Per a això, es realitza repetidament una cerca, augmentant la profunditat de manera incremental. D'aquesta manera sempre tindrem una estimació d'un bon moviment per a l'última profunditat aconseguida, i en cas que s'acabi el temps sempre tindrem assegurada una acció a realitzar. Aquest algorisme és possible gràcies a les taules de transposició, que permeten recuperar els càlculs previs, tot i que s'ha de considerar que, sent un algorisme exponencial, el cost de tornar a avaluar un nivell es petit en comparació amb el cost de l'avaluació del següent nivell si el nivell de ramificació b fos només de 2, el cost seria equiparable, el cost del següent nivell serà b-1 vegades el cost de tots els càlculs fets fins llavors, i el valor tant com b creix, un valor que ja hem aproximat en 36 pels escacs, o 144 per a C'escacs.
Els avantatges addicionals són també importants, característiques que una mica més endavant comprovarem que són de gran importància:
- Permet millorar l'ordenació dels moviments, detectant la variació principal, doncs s'han avaluat les posicions en cada nivell; el cost d'aquesta avaluació és un cost addicional que s'amortitza amb aquest benefici.
- Permet la creació de taules de transposició al menor nivell de profunditat, així com ajustar el valor d'heurístics dinàmics, dos punts a tenir molt en consideració.
- El valor minimax obtingut en el nivell inferior es pot fer servir per a la tècnica de les finestres d'aspiració, definint la finestra de búsqueda a aquests valors.
- Quan en una profunditat menor es troba una solució amb el valor màxim, és a dir, un mat, no es requereix buscar a més profunditat.
Sovint les referències, en comptes de referir-se a minimax, es refereixen a negamax, que senzillament és una simplificació de minimax considerant que és un joc de suma zero per a dos jugadors; aquest algorisme fa servir valoracions positives per a les jugades un jugador i negatives per les jugades de l'oponent. En la pràctica és una implementació de minimax.
La poda alfa-beta és un algorisme de cerca que busca disminuir el nombre de nodes que són avaluats per l'algorisme minimax en el seu arbre de cerca. Deixa d'avaluar una jugada quan s'ha trobat almenys una possibilitat que demostri que la jugada és pitjor que una jugada examinada anteriorment. No és necessari continuar avaluant aquestes jugades. Quan s'aplica a un arbre minimax estàndard, retorna la mateixa jugada que el minimax, però elimina les branques que no poden influir en la decisió final. Això comporta un gran estalvi en la quantitat de càlculs necessaris.
L'algorisme sembla que ha estat reinventat
diverses vegades: Arthur Samuel tenia una versió primerenca per a una simulació de dames; posteriorment Richards, Timothy Hart, Michael Levin i Daniel Edwards varen fer servir conceptes de l'algorisme alfa-beta de manera independent en els EUA, i també McCarthy va proposar idees similars durant el taller de Dartmouth en 1956 i el va suggerir a un grup dels seus estudiants. Finalment, Alexander Brudno, informàtic rus, va concebre l'algorisme alfa-beta de manera independent i va publicar la descripció, funcionament i resultats en 1963. Tot i les aproximacions prèvies, fou Alexander Brudno qui va presentar formalitzada i justificada la idea sencera, que Donald Knuth i Ronald W. Moore varen refinar en 1975.
Millora del cost de l'algorisme minimax
L'efectivitat de l'esporgada té una gran dependència de l'ordre en què s'avaluen les diferents opcions (jugades), de manera que si l'ordre és incorrecte pot arribar a donar-se el cas de no tenir cap benefici, però per a un ordre òptim, avaluant la millor jugada primer, el benefici és radical, permetent l'avaluació del doble de profunditat; és a dir, un cost de O(bd/2). La reducció és dràstica, i considerant els escacs amb un factor de ramificació de 36 es pot arribar a reduir el cost d'exploració per a quatre nivells només a 3_000 nodes, en comptes de milió i mig, una reducció del 99.8%.
Heurístics d'ordenació de les jugades
Per obtenir uns resultats òptims en l'algorisme alfa-beta, es requereix un nou heurístic: l'ordenació de les jugades, considerant primer les més favorables.
L'efectivitat de l'algorisme alpha-beta, que pot resultar dràstica, depèn de l'efectivitat d'aquest heurístic, d'una primera estimació de quina és la millor jugada, que es confirmarà amb l'exploració minimax. Aquest heurístic té una afectació directa en el rendiment de l'algorisme, i, per tant, de la profunditat amb què és possible fer l'anàlisi, però un error en l'ordenació pot arribar a eliminar l'aventatge de la poda alpha-beta, resultant una exploració minimax sense cap optimització.
Es fa servir una ordenació dinàmica, on l'ordenació dels nodes no avaluats es canvia quan s'avaluen els nodes anteriors i obtenim noves informacions per millorar l'heurístic d'ordenació. Sense incloure-hi les situacions d'escac, l'ordenació tindrà en consideració:
- S'ha de considerar l'últim moviment de l'adversari; verificar si segueix la variació principal estimada.
- Si el moviment de l'adversari no ha estat la predicció de la variació principal:
- Considerar si la peça moguda pot ser capturada.
- Considerar igualment el moviment ja estudiat com la variació principal, si encara és vàlid.
- Les amenaces: una peça amenaçada sense defença, o amenaçada per una peça d'igual o inferior valor.
- Si existeix una captura de la peça que amenaça, i l'avaluació estàtica de l'intercanvi és favorable.
- Moviments per evitar aquesta amenaça: moure la peça o cobrir l'amenaça.
- Provocar una amenaça major al contrincant.
- Observar que ignorar l'amenaça fent un sacrifici serà un cas fora del comú, que, en general, sempre seran per seguir una línia guanyadora ja estudiada com a línia principal, o una variació de la línia principal.
- Les captures s'han de pendre en consideració fent servir una avaluació estàtica d'intercanvi per estimar si s'han de considerar.
- L'heurística de l'assassí (killer heuristic), que consisteix en considerar quan s'explora l'arbre de joc que una jugada que era una bona jugada en una posició, és probable que ho segueixi sent en una posició alternativa.
- assassins de mat diferència jugades que produeixen un tall en la búsqueda degut a que un dels jugadors assoleix el mat.
- L'heurística del moviment de resposta, que considera que si existeix un moviment de resposta per a un moviment, sempre que la resposta encara sigui vàlida, molt probablement serà la millor resposta indistintament que s'hagin fet moviments entremitjos.
- L'heurística de l'última millor resposta (LBR, Last Best Reply), bàsicament la mateixa idea que l'heurística del moviment resposta, amb subtils diferències d'implementació. S'ha de fer constar, en ambdós heurístics, que moltes vegades aquestes heurístiques funcionen com a resposta al moviment d'una peça a una posició, indistíntament de la seva posició d'origen.
- L'Heurística de l'història, que fa una ordenació dinàmica dels moviments considerant el nombre de talls causats per un moviment determinat, independentment de la posició en la qual s'hagi realitzat aquest moviment.
Heurístics de poda en davant
La poda alpha-beta estableix que alguns nodes no requereixen ser avaluats, doncs no són opcions a considerar, però sempre, la creença en aquest fet, depèn de l'heurístic d'avaluació. A més, trobar eficientment els nodes que no requereixen avaluació depèn de la correcta ordenació, avaluant primer els nodes més significatius, que tenen les jugades millors.
La poda alpha-beta, encara que la seva eficiència depén d'un heurístic d'ordenació, no és un heurístic, és un algorisme que permet la simplificació de branques que no aportan informació. Les podes en davant són heurístics que permeten descartar nodes sense motius plenament justificats, només per certes creences
. Veiem tècniques que són indicadors de branques de búsqueda que no aportaran nova informació, i poden deixar de considerar-se:
Generació d'un moviment buit, és a dir, un canvi de torn sense cap moviment. Tot i no ser una acció vàlida en el joc, en el motor de cerca resulta d'utilitat; es fa servir en el node arrel amb una cerca limitada en profunditat.
- Permet establir ràpidament un primer límit inferior (beta) per a la finestra de búsqueda.
- També permet detectar moviments assassins i captures de l'adversari que refuten aquest moviment buit.
Aquesta tècnica es basa en el fet que, en escacs, no moure condueix a una situació pitjor que fer una jugada correcta, excepte en comptades excepcions, denominades Zugzwang. Aquestes situacions de Zugzwang són extranyes, encara més extranyes en C'escacs que en els escacs ortodoxos, malgrat es donen amb més freqüència en la part final del joc, quan queden poques fitxes.
- El problema és detectar les situacions de Zugzwang, i per fer-ho existeix la tècnica del doble moviment buit; un segon moviment buit restaura la situació de joc anterior al primer moviment buit, és a dir, la situació arrel inicial, però ara en una situació de búsqueda més limitada en profunditat.
- En el mig joc l'anàlisi del doble moviment buit resulta massa costòs, i el Zugzwang una situació molt extranya, però sí és convenient tenir-ho en consideració en l'etapa final del joc, quan el Zugzwang és més freqüent.
Podes d'inutilitat: Aquesta poda es basa en el valor d'alpha, estimant quan una branca no té potencial d'obtenir un valor suficientment alt. A més, permet fer un càlcul incremental de l'heurístic d'avaluació: Com es coneix el valor d'alpha que s'ha d'obtenir per tenir en consideració la branca, es pot avaluar primer els trets que més afecten al valor final, com les fitxes de cada jugador, i algunes condicions posicionals més subtils i costoses d'avaluar no es requereix que siguin avaluades si el valor no arriba a mínim significatiu, sumant-hi amb un marge màxim.
Típicament aquesta poda es fa en els nivells més inferiors de la búsqueda, podant només un nivell, però els programes més actuals opten per incrementar el número de nivells afectats per la poda en els moviments que ha s'han considerat com a menys favorables, és a dir, posicionats al final de l'ordenació.
- Podes delta: En la búsqueda de quiescència, les podes delta fan servir les avaluacions estàtiques d'intercanvi per descartar una jugada si el benefici estimat de l'intercanvi més un petit marge encara és insuficient per prendre en consideració el node. És molt semblant a les podes d'inutilitat, però en el context de la búsqueda de la quiescència.
Reducció del moviment tardà: Descartar els moviments menys prometidors, és a dir, els que són al final de l'ordenació. En realitat no es tracta de descartar-los del tot, encara que algunes versions modernes basades en xarxes neuronals (Evolving Neural Networks to Focus Minimax Search, 1994, David Moriarty) sí fan directament una reducció dels nodes a considerar, però la tècnica a què ens referim només fa una reducció en el nivell d'exploració d'aquests nodes poc prometidors.
Com que normalment aquests nodes no produeixen bons resultats, no tindran potencial d'incrementar α i es podria reduir el temps que s'ocupa a explorar aquests nodes. Això és oposat a la poda de moviment buit que tracta de trobar valors que superin el límit de β.
Es realitza una cerca de finestra mínima per cada moviment poc prometedor, pel fet que només es desitja comprovar si el moviment pot superar el límit inferior α. Per a realitzar aquesta cerca es fa ús d'una reducció en la profunditat de cerca. Si l'avaluació torna una valor inferior a α indica que el moviment serà pobre i no valdrà la pena invertir més temps determinant el seu valor. Si la cerca torna un valor superior a α, indica que existeix alguna cosa interessant en la posició, i s'ha de realitzar la cerca amb els límits reals de la finestra de cerca i utilitzar la profunditat regular.
El mateix que en les podes d'inutilitat, en les reduccions dels moviments tardans és convenient fer servir un càlcul dinàmic de l'heurístic d'avaluació. Els programes actualment fan servir profunditats de poda més grans en tant els moviments han quedat ordenats per a ser considerats més tardanament, combinant-les amb finestres mínimes de cerca.
Tot i que aquesta poda en un inici es limitava a una poda de l'últim nivell, sense cap altra reducció de profunditat, s'ha anat incrementant el seu ús en tant s'ha verificat la seva efectivitat, particularment quan es fa servir conjuntament amb tècniques d'ordenació dinàmiques.
Llibres d'obertures i finals
Els punts més febles dels algorismes minimax són les obertures i els finals, envers dels bons resultats en el joc mig. Es dona el cas que obertures i els finals són punts ja ampliament estudiats per la teoria dels escacs. Les obertures permeten una correcta distibució inicial que difícilment es pot aconseguir amb l'estudi del joc a curt termini, i és per això que els programes d'escacs compten amb un llibre d'obertures.
Anàlogament, els finals comporten dificultats per la profunditat d'anàlisi que requereixen; les taules de transposició combinades amb les consideracions de simetria de l'escaquer són fonamentals per a un anàlisi que pot requerir una gran profunditat d'exploració, doncs, malgrat que el nombre de ramificació sigui més limitat que en la fase mitja del joc, un anàlisi amb gran profunditat d'exploració encara és una opció inabastable sense aquestes eines. Tot i això, el càlcul de finals és molt costòs i les bases de taules (tablebase) de finals de joc permeten tenir els moviments òptims precalculats. Iniciades per Thomas Ströhlein en 1970 amb els finals KQK, KRK, KPK, KQKR, KRKB i KRKN. Ken Thompson i altres les van completar per a tots els finals de quatre i cinc peces, amb els casos particulars KBBKN, KQPKQ i KRPKR. En 2005 s'havien completat tots els finals amb fins a sis peces, en 2018 amb set peces (els dos reis i cinc altres peces), i actualment, en 2023, encara es treballa per obtenir tots els finals amb vuit peces.
Millores a minimax i alfa-beta
L'algorisme minimax amb la poda alfa-beta és l'algorisme que s'ha fet servir per als programes d'escac d'ordinador des dels anys 70 del segle XX fins ja entrat el segle XXI. Els programes van anar incorporant característiques, com la búsqueda de la quiescència o la confirmació de jugades prometerdores, incrementant la profunditat de búsqueda en alguns punts, les taules de transposició, que emmagatzemen posicions ja estudiades per no tornar-les a considerar, els llibres d'obertures, les bases de taules de finals... També la poda alfa-beta ha incorporat millores, pràcticament totes fonamentades en les tècniques d'estretament de la finestra de búsqueda, fixant un valor per a alfa-beta, en comptes de calcular-ho, de manera que tots els nodes amb una avaluació dins d'aquesta finestra alfa-beta establerta no són avaluats. El cas més senzill és la búsqueda por aspiració, on es treu partit de la profunditat iterativa per obtenir una estimació dels valors alpha i beta. Tot i que és una tècnica fonamentada en heurístics, no afecta el resultat final, doncs quan el valor no es troba en la finestra estimada detectarem l'error, i ens veurem obligats a tornar a avaluar per obtenir els valors correctes. Les finestres nul·les són una tècnica semblant, però en aquest cas no es deixa marge entre els valors alpha i beta, quan estimem que el moviment no generarà alteracions d'aquests valors, amb l'intenció de detectar els casos que no compleixin les nostres estimacions. Aquesta tècnica es feia servir tant per anàlisis de quiescència, o per la poda dels moviments tardans, però finalment ha evolucionat en el PVS i finalment en el MTD(f).
La PVS: Principal variation search (NegaScout) estableix una jugada com a millor jugada, i mira de demostrar que la resta de jugades no són millors fent la búsqueda de les altres jugades amb una finestra nul·la; la dependència de l'heurístic d'ordenació de les jugades esdevé encara més fonamental, doncs una incorrecta ordenació resulta en la penalització del cost final de l'algorisme.
PVS es va fer servir des de la seva aparició en l'any 1980, fins l'aparició de MTD(f), Memory-enhanced Test Driver with value f en l'any 1994. Aquest nou algorisme fa servir tota la búsqueda amb una finestra nul·la o molt estreta, partint d'una estimació inicial del valor; la finestra alfa-beta s'estableix en una petita variació d'aquesta estimació final i, considerant que la finestra de búsqueda és molt estreta, moltes branques no requereixen avaluació. Si l'algorisme retorna un valor fora de la finestra establerta s'ha de tornar a fer l'avaluació ampliant la finestra; els nodes ja avaluats es troben a una taula de transposició, per evitar haver de tornar a fer la seva exploració.
Actualment el millor programa per a jugar a escacs amb aquest enfocament d'algorisme clàssic (minimax amb heurístics i algorismes de desbroçament) és el programa Open Source Stockfish, que, en el moment de revissar aquest text ja es troba en la versió 15.1. La versió Stockfish 8 va ser derrotada en desembre de 2017. Havia arribat l'era de la cerca de Montecarlo i les xarxes neuronals en els escacs, i era el final dels tan patits heurístics i desbroçaments alfa-beta.
Les tècniques minimax requereixen un heurístic d'avaluació, i les tècniques alfa-beta un haurístic addicional d'ordenació; les tècniques de millora de la poda alfa-beta requereixen a més a més un oracle que faci una estimació del valor de l'heurístic d'avaluació que s'obtindrà per poder estretar la finestra... El problema és que els heurístics són estimacions que intenten formular el coneixement expert, però són difícils d'establir, a més a més considerant que la manera de veure el problema un expert, generalment molt adaptable a diferents situacions, no sempre coincideix amb els requeriments, molt fixes d'un algorisme; resumint: un algorisme amb fortes dependències d'un heurístic té grans debilitats.
L'enfocament més conservador
podria ser incorporar un sistema d'aprenentatge per a aquest heurístic, per a provar d'obtenir-ho empíricament, però un joc es resistia a l'enfocament minimax durant anys; aquest joc era el Go, que té un factor de ramificació molt alt, de l'ordre d'entre 150 i 250 moviments diferents possibles per a cada jugador, degut al seu tauler quadrat amb 19 caselles per costat, fent un total de 361 caselles, més del doble en caselles que C'escacs.
El mètode de cerca de Montecarlo consisteix en fer servir un mostreig al·leatori, per a casos on no és possible una altra tècnica. i data dels anys 1940. Però va ser en 1987 que Bruce Abramson va combinar la búsqueda minimax amb continuacions aleatòries fins el final de la partida, en comptes de fer servir una funció heurística d'avaluació.
Aquestes tècniques varen ser també molt útils per millorar els algorismes de demostració automàtica de teoremes, una altra aportació de la teoria de jocs a altres branques que es poden considerar més serioses
, de la mateixa manera que minimax s'ha generalitzat al camp de la presa de decisions.
B. Brügmann va fer servir l'algorisme per resoldre el problema del joc del Go en 1992. No va ser fins a 2006 que Rémi Coulom va descriure l'aplicació del mètode de Montecarlo a la búsqueda d'arbres de joc, i el va anomenar com a cerca de Montecarlo. L. Kocsis i Cs. Szepesvári desenvoluparen l'algorisme UCT (Upper Confidence bounds applied to Trees).
Deepmind, adquirida per Google en 2014, en 2015 presentà AlphaGo, el primer programa que derrota un humà al Go en nivell campionat, i en març de 2016 es declarà campió.
L'algorisme consta de quatre fases:
- Selecció: Es parteix de l'arrel R i es van seleccionant successivament nodes fills fins a arribar a un node fulla L.
- L'arrel és l'estat actual del joc i una fulla és qualsevol node que tingui un fill potencial del qual encara no s'ha iniciat cap simulació (playout).
- Expansió: Tret que L acabi la partida de manera decisiva (victòria/pèrdua/empati), crea un (o més) nodes fills i tria el node C d'un d'ells. Els nodes fills són qualsevol moviment vàlid des de la posició de joc definida per L.
- Simulació: Completa una jugada aleatòria des del node C. Aquest pas també es denomina a vegades playout o rollout. Una playout pot ser tan simple com triar moviments aleatoris uniformes fins que es decideixi la partida (per exemple, en escacs, la partida es guanya, es perd o s'empata).
- Retropropagació: Utilitza el resultat del playout per a actualitzar la informació en els nodes del camí de C a R.
El gran aventatge d'aquest algorisme és que no existeix cap dependència d'heurístics, tot i que es poden fer servir sesgant el comportament aleatori per mirar de millorar-ho.
L'inconvenient més gran és que requereix una gran potència de càlcul per a l'entrenament de la xarxa neuronal. Per a decrementar la potència de càlcul requerida per a l'entrenament es pot començar amb un comportament inicial fonamentat en heurístics, i fer servir la xarxa neuronal únicament per a l'aprenentatge d'un nivell superior de coneixement del joc. Preferiblement aquests heurístics hauran de ser senzills i efectius, per evitar sobrecostos i biaixos.
Deepmind: AlphaZero i MuZero
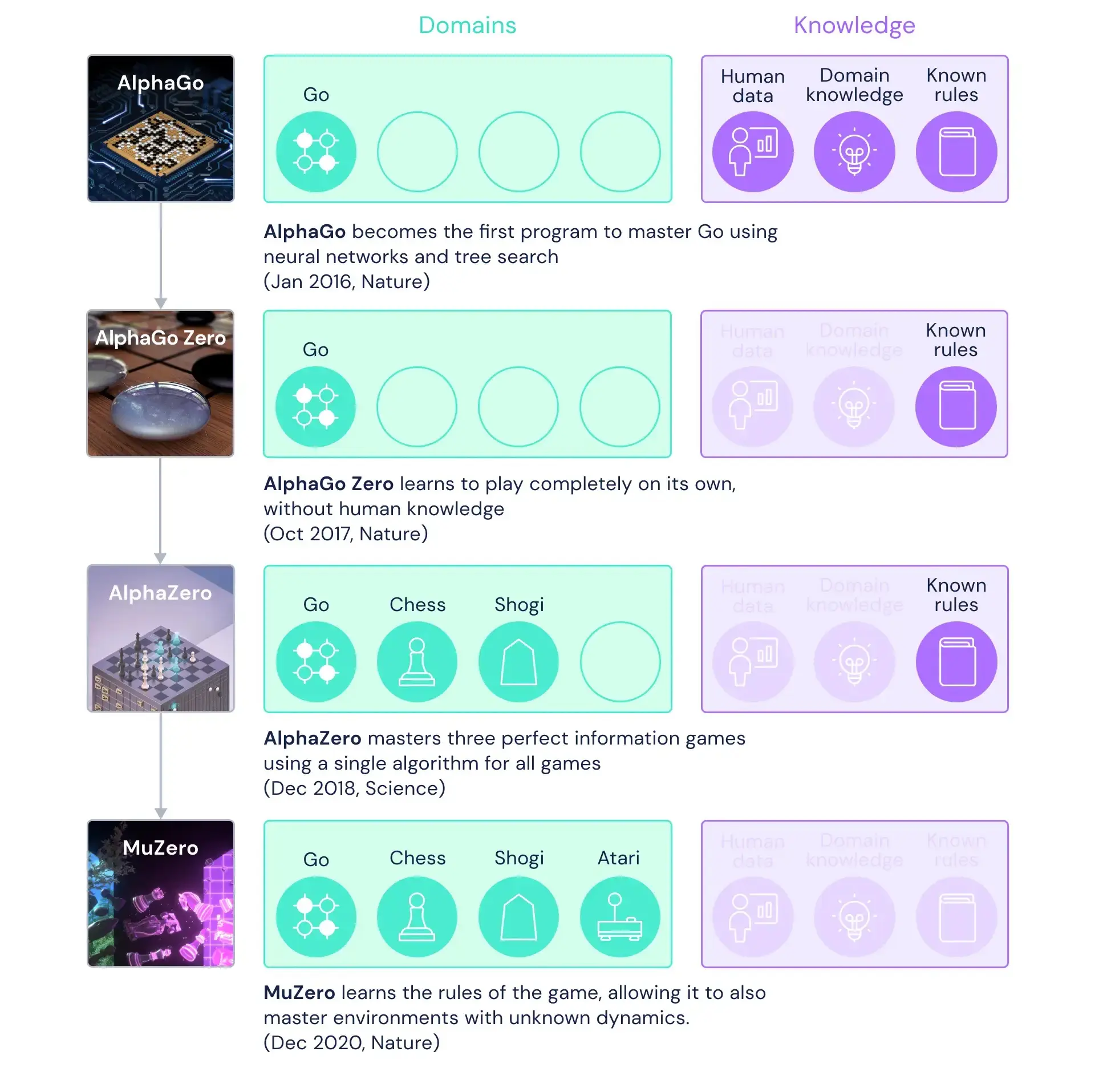d'AlphaGo a MuZeroAlphaGo fou el primer programa de jugar a Go a nivell de mestre, aconseguint el títol de campió del món en 2016. El programa incorporava coneixement específic per a la incorporació d'heurístics, i havia aprés
amb una gran base de dades existent amb partides.
L'experiència d'AlphaGo es va aprofitar per construir AlphaGo Zero, que ara només tenia coneixement de les regles del joc, sense cap altre mena d'heurístic ni coneixement específic del joc. El programa havia aprés
jugant partides simulades contra ell mateix, fent servir una tècnica d'aprenentatge per reforç.
AlphaGo Zero es va generalitzar a AlphaZero, que era capaç de jugar a diferents jocs: els escacs i el Shogi, a més del Go, tot només incorporant les regles del joc. Aquest programa aviat va guanyar al millor programa que feia servir les tèniques minimax tradicionals, amb poda alfa-beta i moltes altres tècniques que s'havien desenvolupat al llarg dels anys, però totes elles fortament fonamentades en l'existència d'heurístics.
Aquest programa fa servir una cerca de Montecarlo incorporant aprenentatge del joc per reforç per a programar una xarxa neuronal d'aproximadament vuitanta nivells, sumant un total de centenars de milers de nodes (neurones
).
Podem veure com algunes de les tècniques d'escacs d'AlphaZero han sorprés fins i tot els grans experts dels escacs, doncs els moviments, no tan limitats
pels heurístics que s'exigeixen als programes d'escacs, sovint són inesperats i sorprenents. En el blog zugzwang podem veure quatre exemples comentats d'aquest desafiament. També podem veure comentada una partida d'un posterior desafiament en desembre de 2018, d'una versió renovada d'AlphaZero contra la mateixa versió Stockfish 8, tot i ja existir la versió 10 del programa. º
És cert que, tot i que inicialment AlphaZero va derrotar el millor programa del moment, Stockfish 8, es critica el desequilibri en el maquinari que han fet servir les dues parts. Stockfish incorpora millores en les seves successives versions, en el moment d'escriure aquest text, la versió 15.1. També AlphaZero ha incorporat millores; la versió d'alpha-zero actual és la 16, però una versió d'un codi que ja no pertany a Deepmind Google, sinó reproduccions implementades per tercers, però ens permet veure algunes partides més, doncs la versió de Deepmind ha deixat d'estar accessible:
En 2019 DeepMind publicà un nou artícle on detalla MuZero, un nou algorisme capaç de generalitzar AlphaZero, per a jugar a jocs de taula i jocs Atari (Arcade) sense conèixer les regles o representacions del joc; el programa MuZero fa servir tres xarxes neuronals, en comptes d'una sola, i no ha millorat a AlphaZero, però l'ha igualat sense tenir informació del joc. Com s'ha comentat, la versió d'AlphaZero ja no és mantinguda per Deepmind Google, però s'han desenvolupat clons des de la informació que es va publicar.
Algunes referències addicionals
- How Computers Play Chess, 1990, D.N.L. Levy, Monty Newborn. Ed W.H.Freeman & Co Ltd.
- Chess Programming Wiki
- Desarrollo de un motor de ajedrez. Algoritmos y heurísticas para la reducción del espacio de búsqueda. Bachelor Thesis. Omar Edgardo, L. S. 2010
- https://stockfishchess.org/
- Stockfish: configuración, descarga y secretos
- Stockfish 15.1: nueva versión todavía más fuerte
- AlphaZero: Analizamos sus mejores jugadas de ajedrez en el match contra Stockfish
- Minimax and Monte Carlo Tree Search
- Wikipedia: Monte Carlo tree search
- Monte Carlo Tree Search: An Introduction
- AlphaZero Resources (DeepMind)
- Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm
- AlphaZero Chess: How It Works, What Sets It Apart, and What It Can Tell Us
- A Simple Alpha(Go) Zero Tutorial
- MuZero: The Walkthrough (Part 1/3)
- MuZero: The Walkthrough (Part 2/3)
- MuZero: The Walkthrough (Part 3/3)
